Puzzle 12: Dot Product

Overview

Implement a kernel that computes the dot product of vector a and vector b and stores it in output (single number). The dot product is an operation that takes two vectors of the same size and returns a single number (a scalar). It is calculated by multiplying corresponding elements from each vector and then summing those products.

For example, if you have two vectors:

\[a = [a_{1}, a_{2}, …, a_{n}] \] \[b = [b_{1}, b_{2}, …, b_{n}] \]

​Their dot product is: \[a \cdot b = a_{1}b_{1} + a_{2}b_{2} + … + a_{n}b_{n}\]

Note: You have 1 thread per position. You only need 2 global reads per thread and 1 global write per thread block.

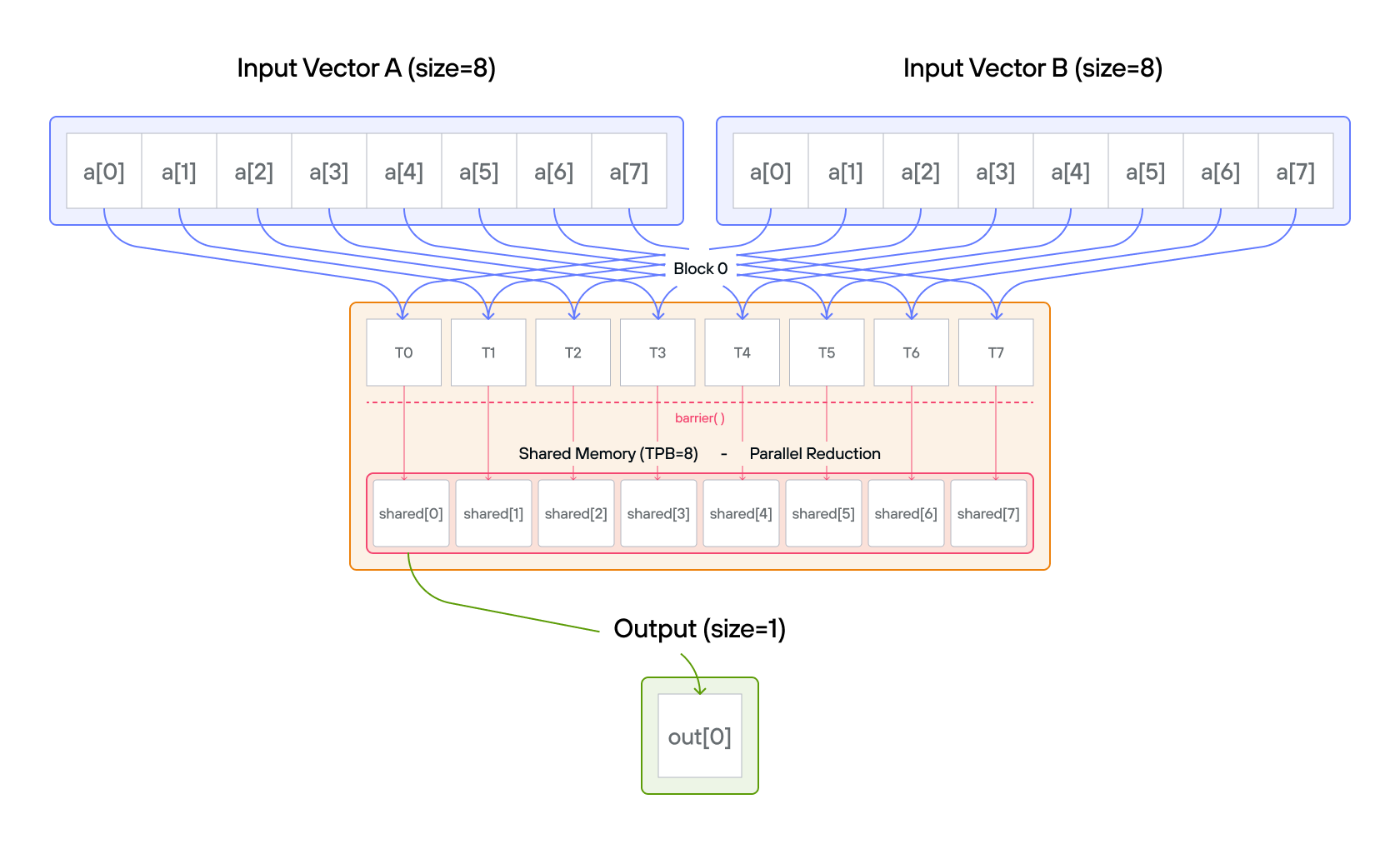
Implementation approaches

🔰 Raw memory approach

Learn how to implement the reduction with manual memory management and synchronization.

📐 LayoutTensor Version

Use LayoutTensor’s features for efficient reduction and shared memory management.

💡 Note: See how LayoutTensor simplifies efficient memory access patterns.