Puzzle 13: 1D Convolution
Moving to LayoutTensor
So far in our GPU puzzle journey, we’ve been exploring two parallel approaches to GPU memory management:
- Raw memory management with direct pointer manipulation using UnsafePointer
- The more structured LayoutTensor with its powerful address_space parameter for memory allocation
Starting from this puzzle, we’re transitioning exclusively to using
LayoutTensor. This abstraction provides several benefits:
- Type-safe memory access patterns
- Clear representation of data layouts
- Better code maintainability
- Reduced chance of memory-related bugs
- More expressive code that better represents the underlying computations
- A lot more … that we’ll uncover gradually!
This transition aligns with best practices in modern GPU programming in Mojo 🔥, where higher-level abstractions help manage complexity without sacrificing performance.
Overview
In signal processing and image analysis, convolution is a fundamental operation that combines two sequences to produce a third sequence. This puzzle challenges you to implement a 1D convolution on the GPU, where each output element is computed by sliding a kernel over an input array.
Implement a kernel that computes a 1D convolution between vector a and vector b and stores it in output using the LayoutTensor abstraction.
Note: You need to handle the general case. You only need 2 global reads and 1 global write per thread.
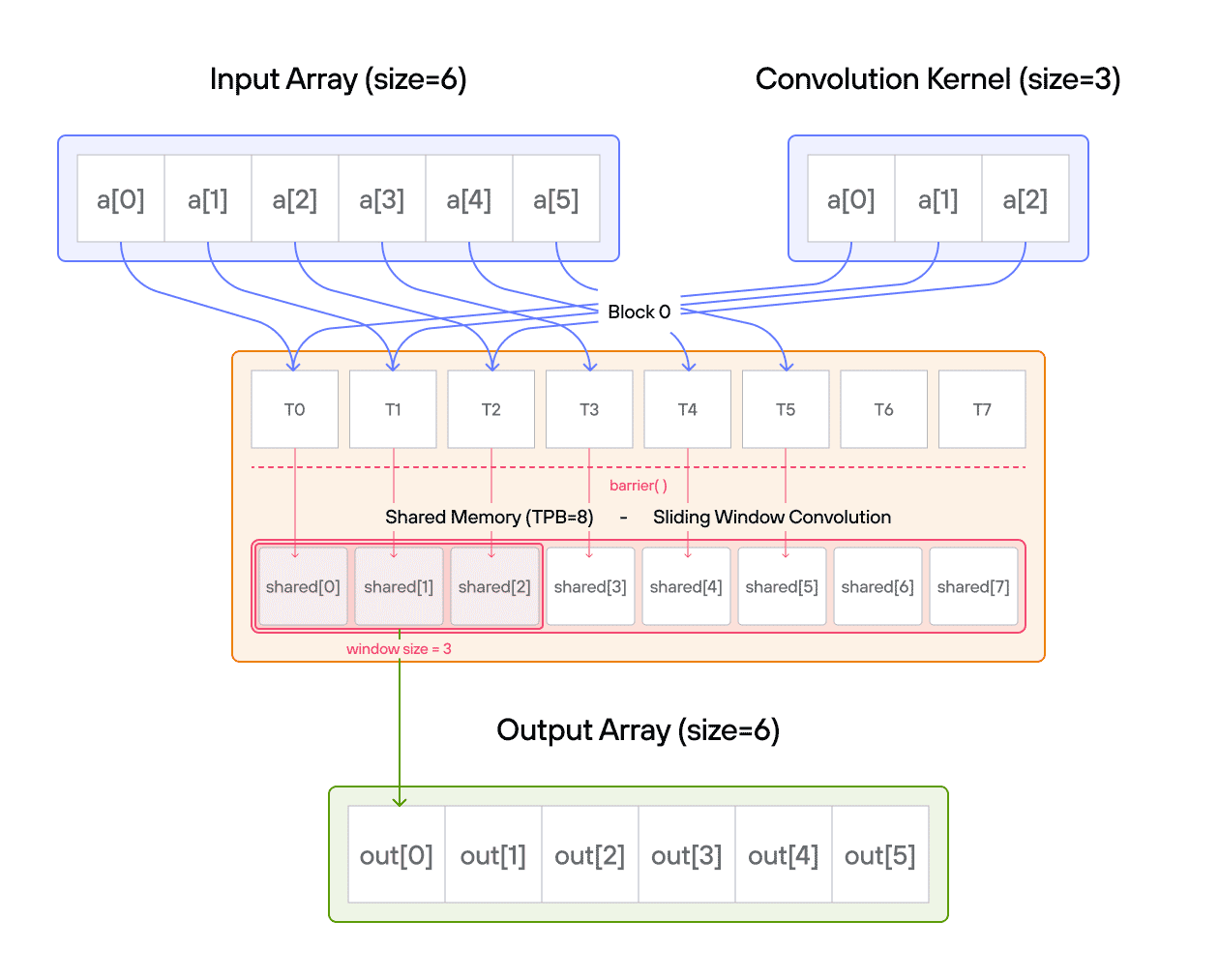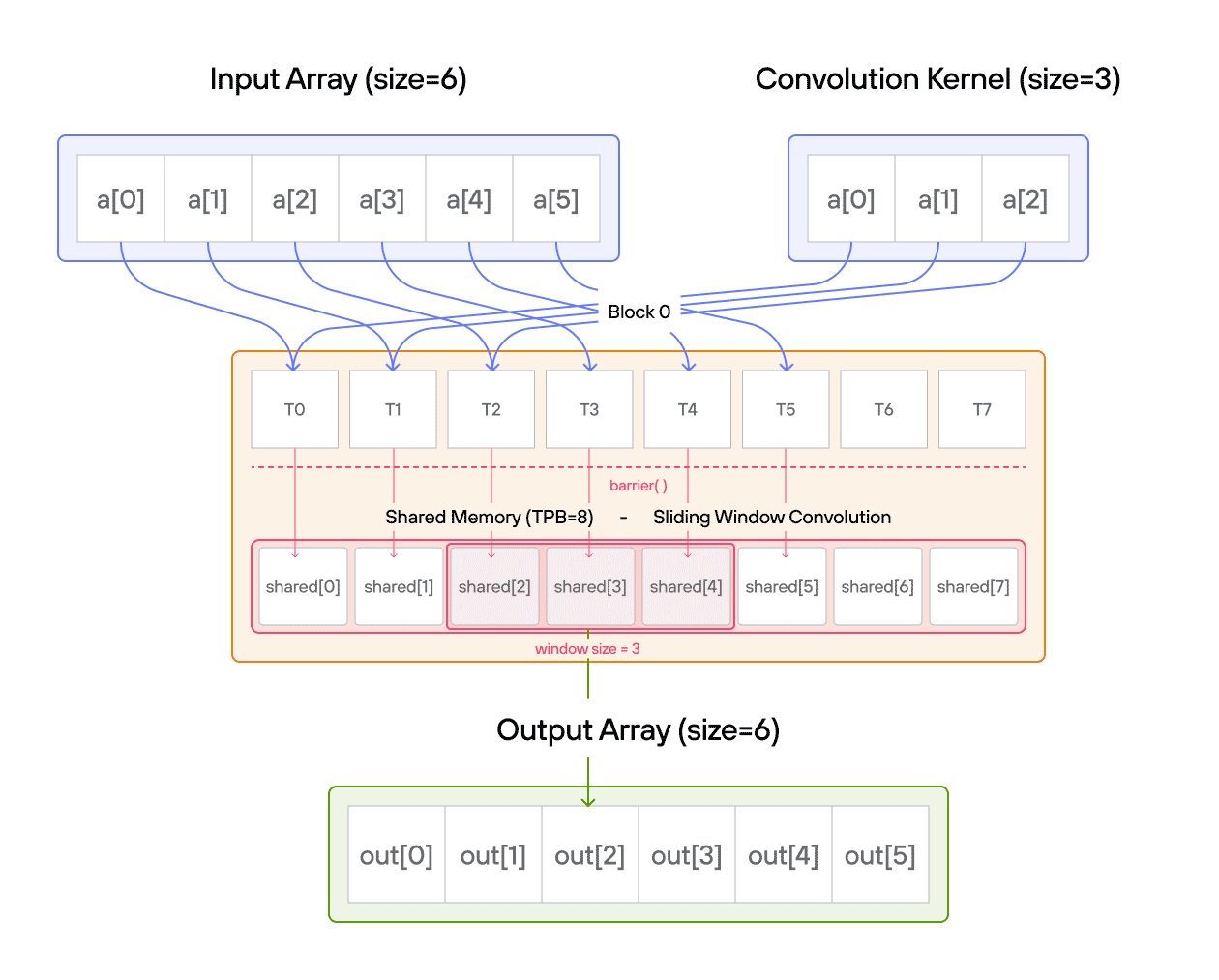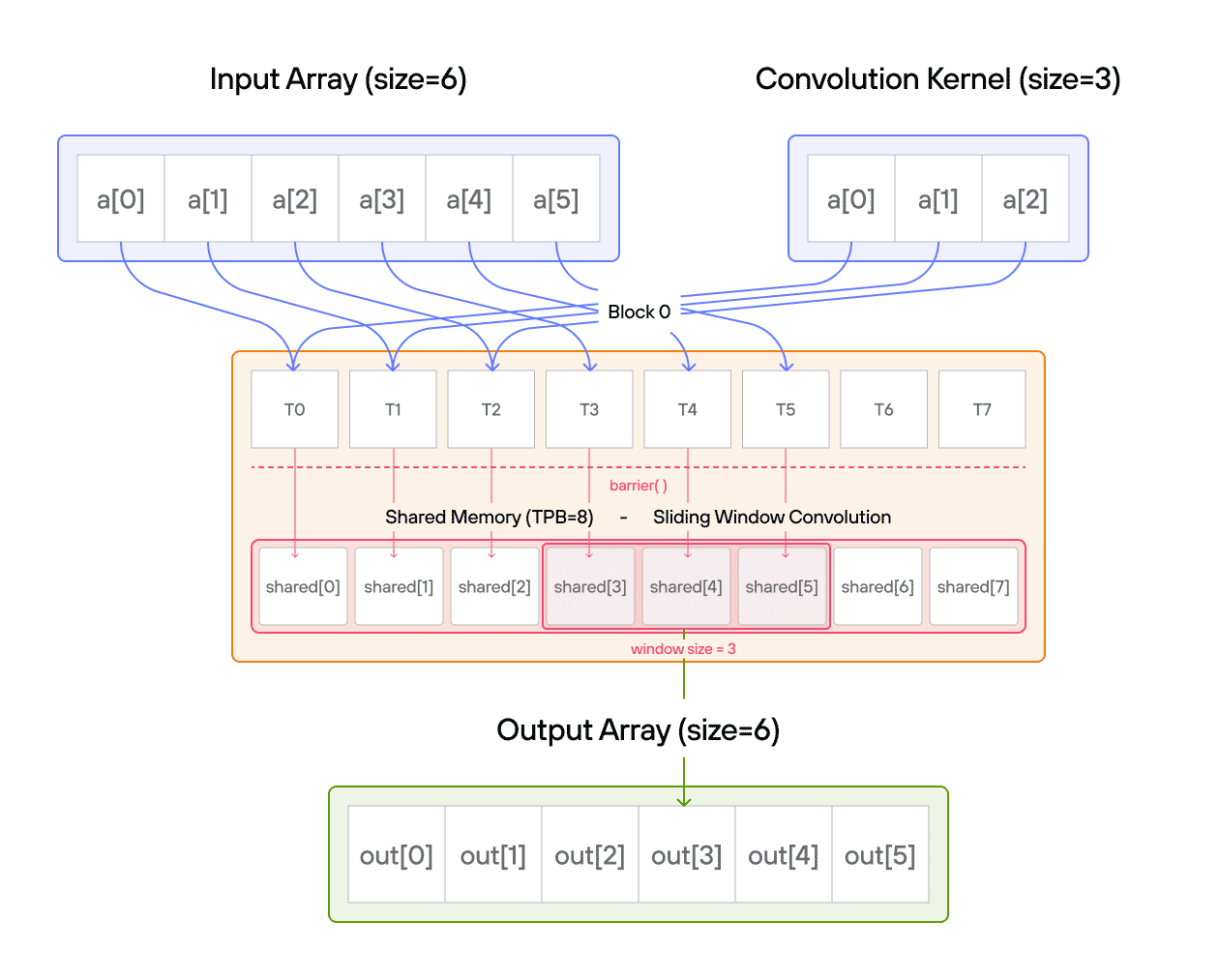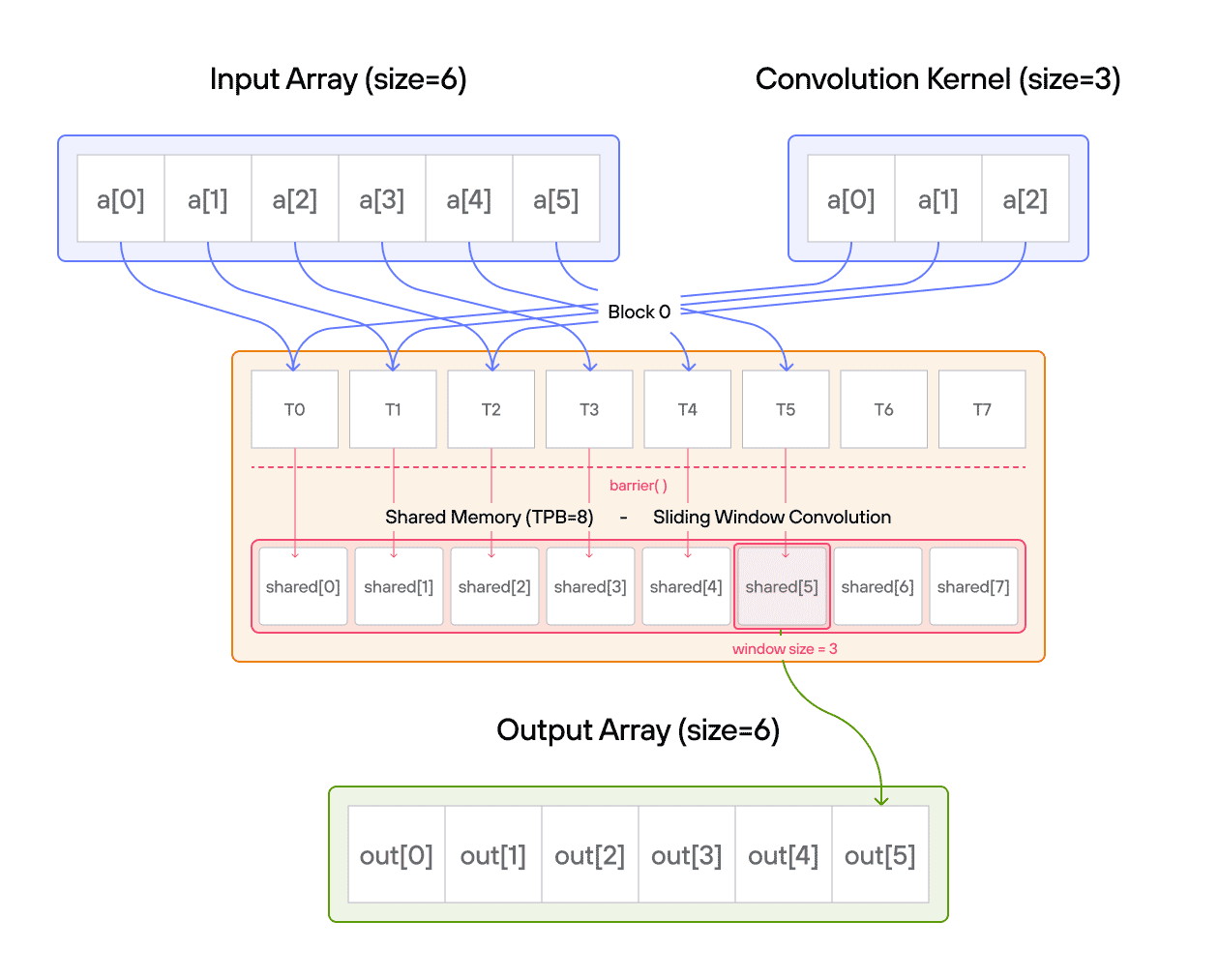
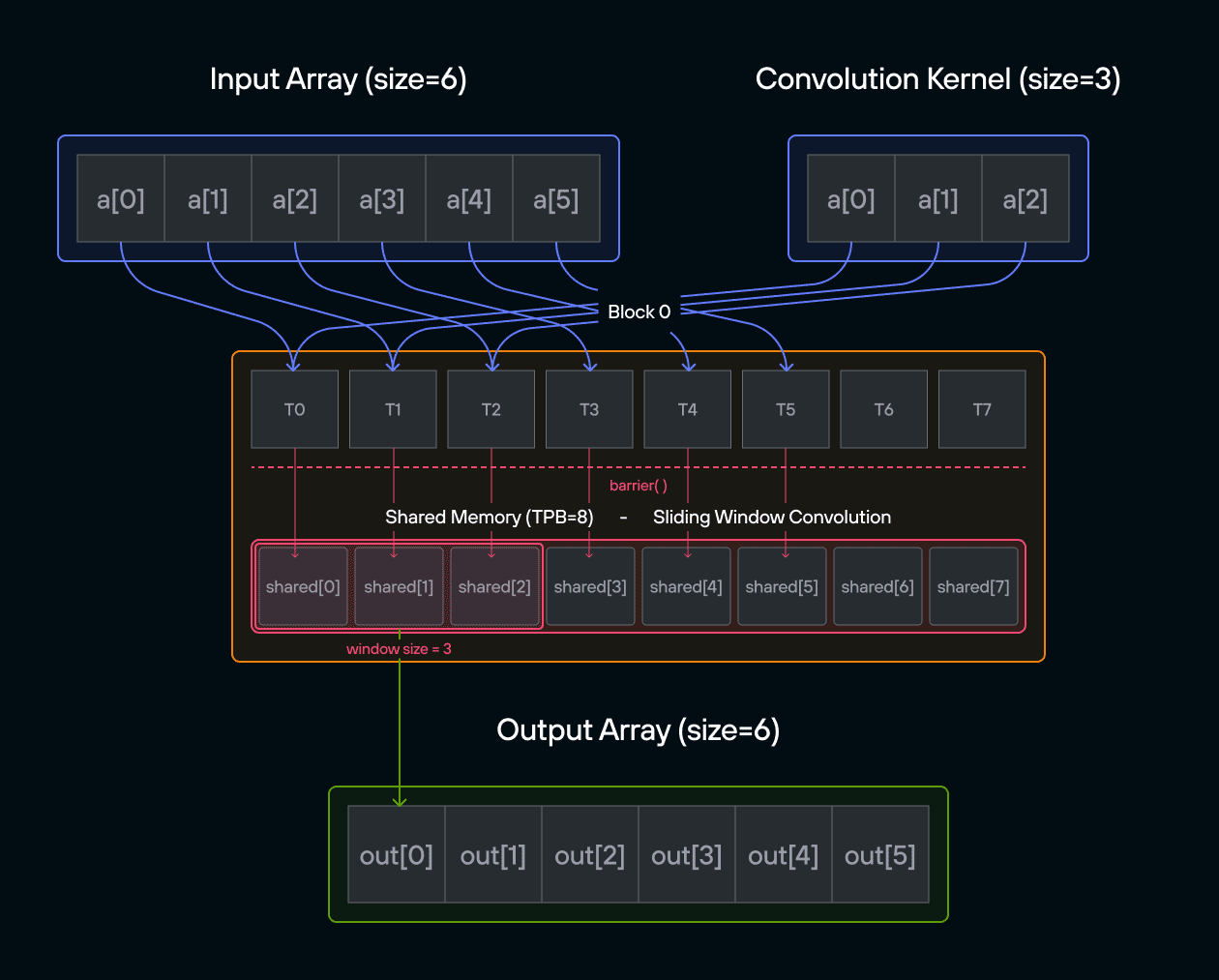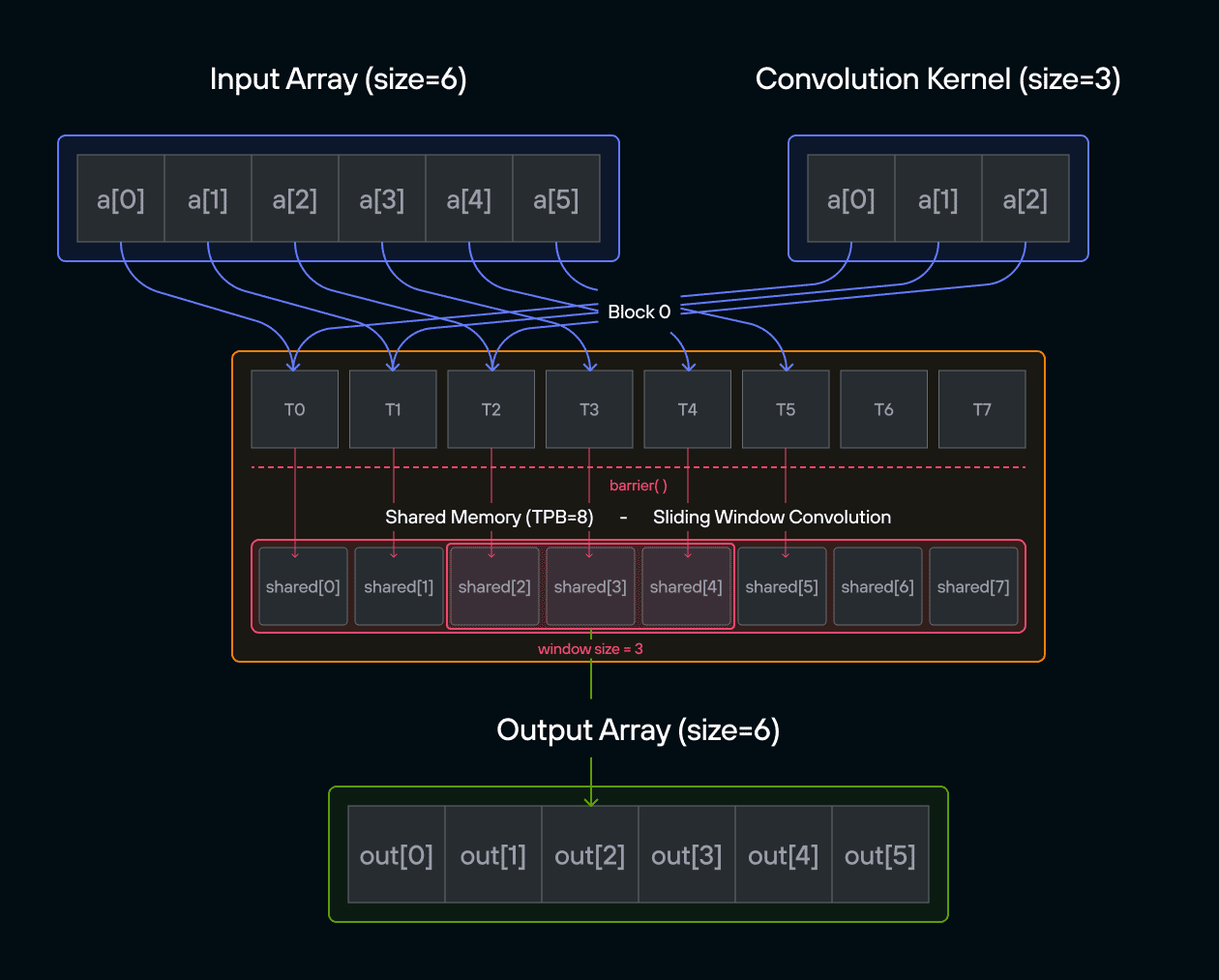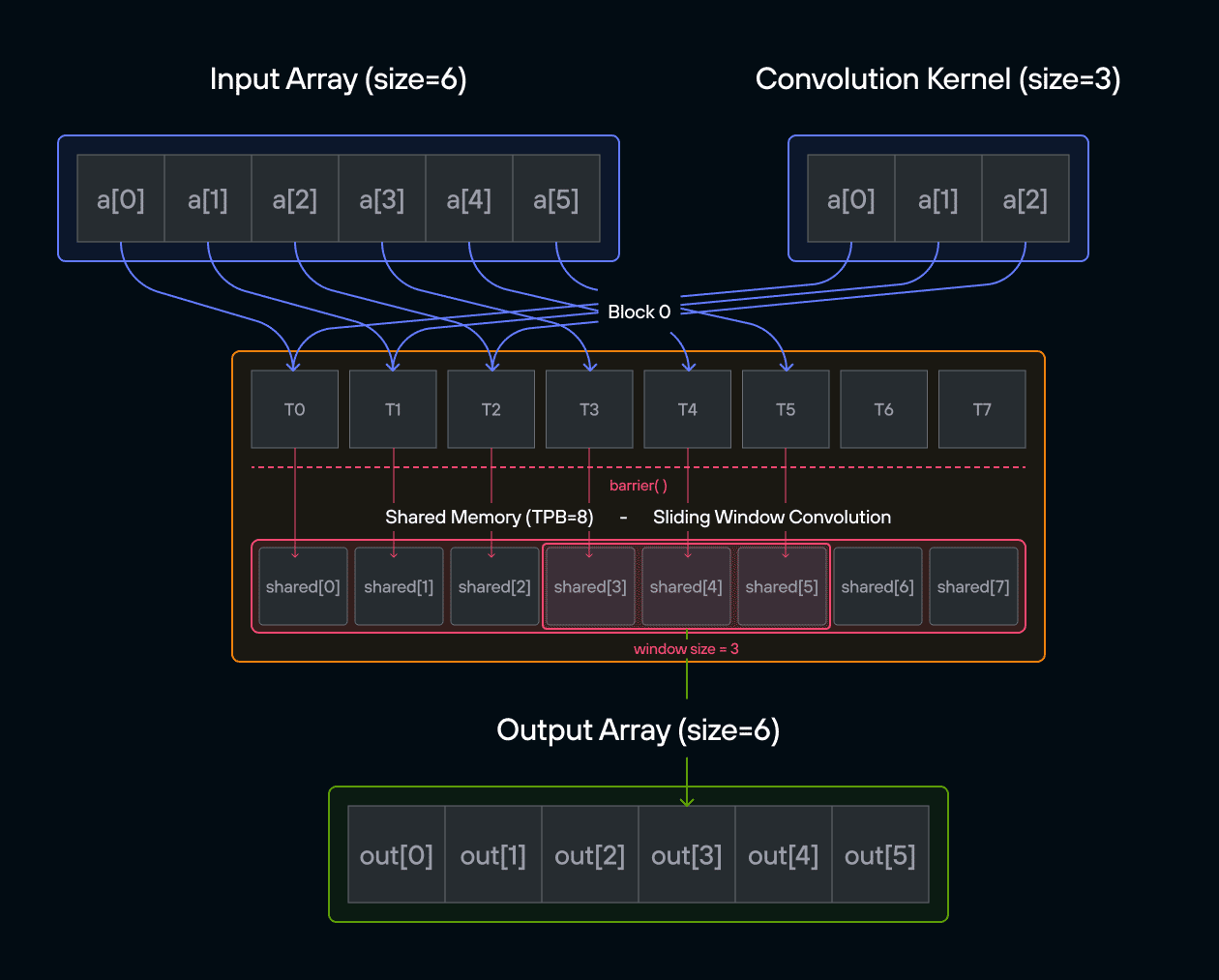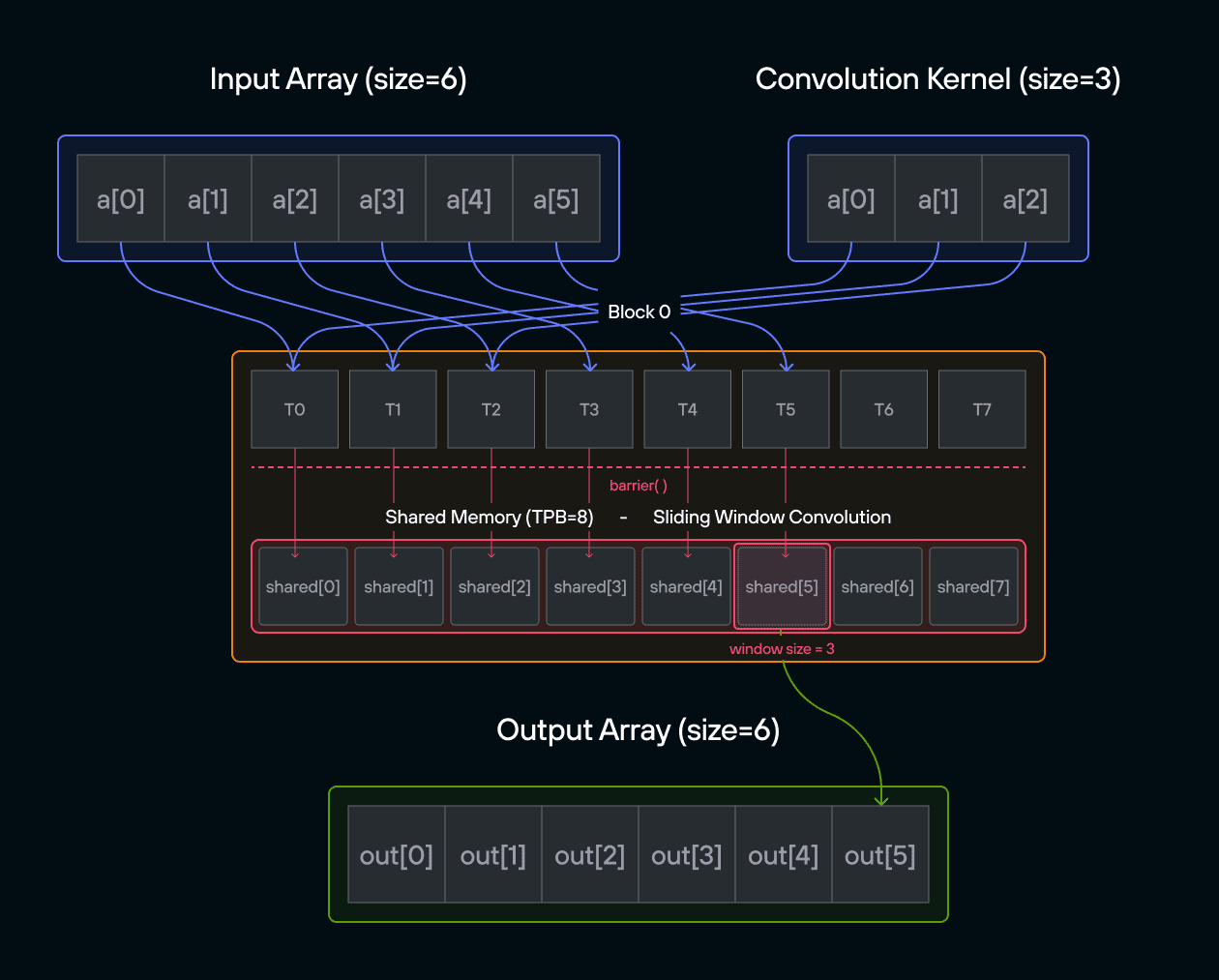
For those new to convolution, think of it as a weighted sliding window operation. At each position, we multiply the kernel values with the corresponding input values and sum the results. In mathematical notation, this is often written as:
\[\Large output[i] = \sum_{j=0}^{\text{CONV}-1} a[i+j] \cdot b[j] \]
In pseudocode, 1D convolution is:
for i in range(SIZE):
for j in range(CONV):
if i + j < SIZE:
ret[i] += a_host[i + j] * b_host[j]
This puzzle is split into two parts to help you build understanding progressively:
-
Simple Version with Single Block Start here to learn the basics of implementing convolution with shared memory in a single block using LayoutTensor.
-
Block Boundary Version Then tackle the more challenging case where data needs to be shared across block boundaries, leveraging LayoutTensor’s capabilities.
Each version presents unique challenges in terms of memory access patterns and thread coordination. The simple version helps you understand the basic convolution operation, while the complete version tests your ability to handle more complex scenarios that arise in real-world GPU programming.