Puzzle 14: Prefix Sum

Overview

Prefix sum (also known as scan) is a fundamental parallel algorithm that computes running totals of a sequence. Found at the heart of many parallel applications - from sorting algorithms to scientific simulations - it transforms a sequence of numbers into their running totals. While simple to compute sequentially, making this efficient on a GPU requires clever parallel thinking!

Implement a kernel that computes a prefix-sum over 1D TileTensor a and stores it in 1D TileTensor output.

Note: When a is larger than the block size, the simple version only stores the sum of each block, while the complete version synchronizes across blocks to produce the full prefix sum.

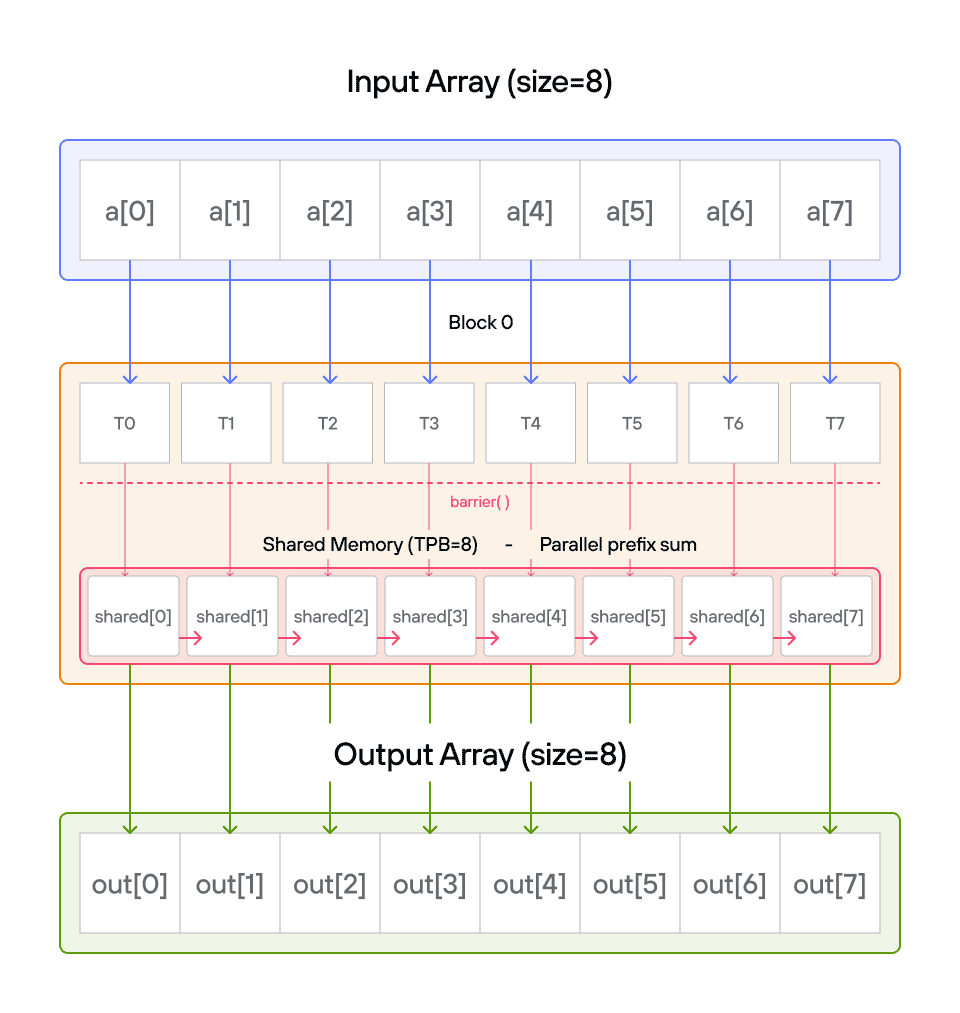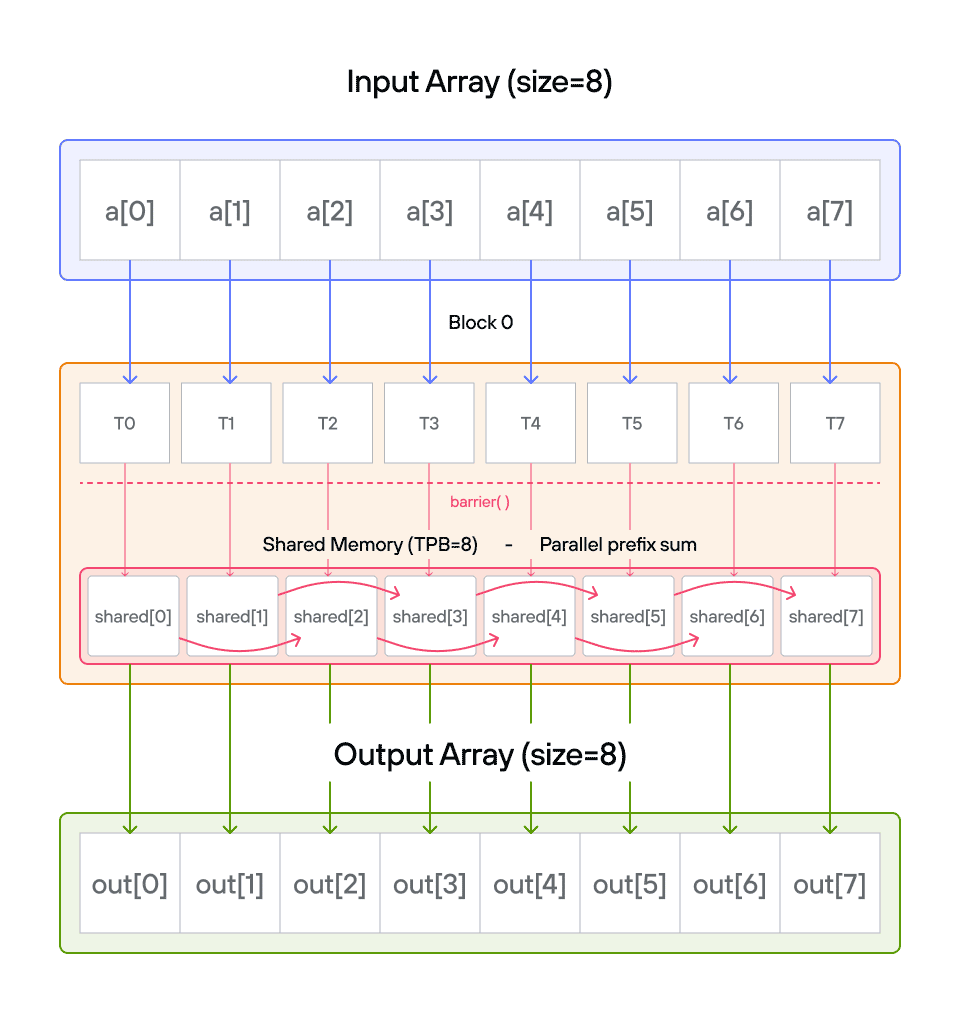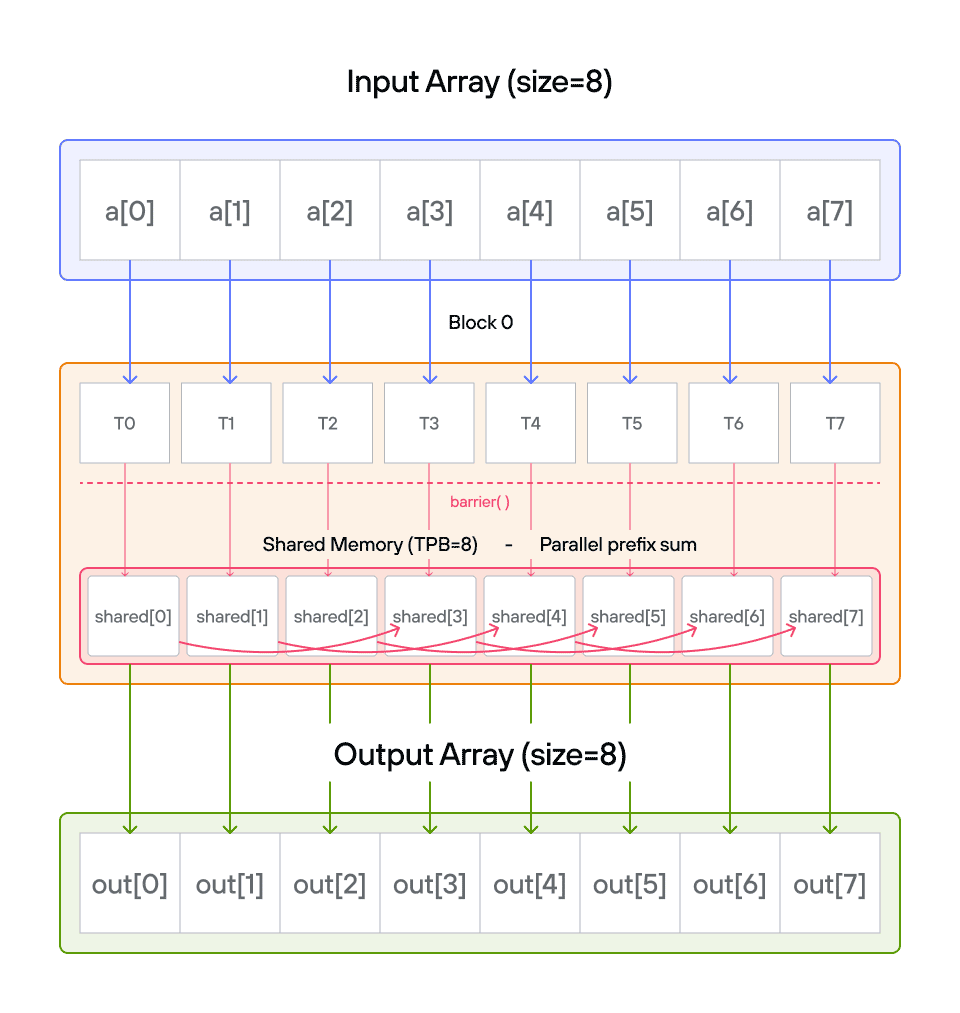
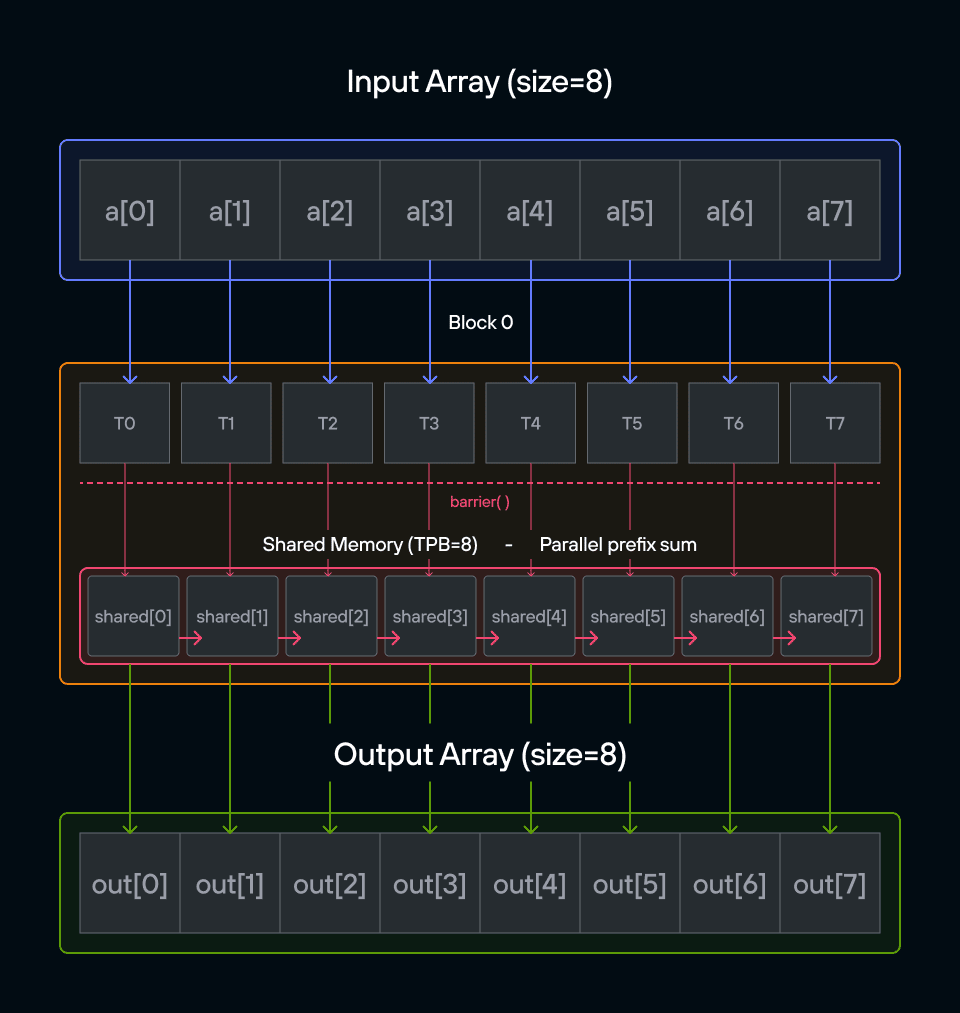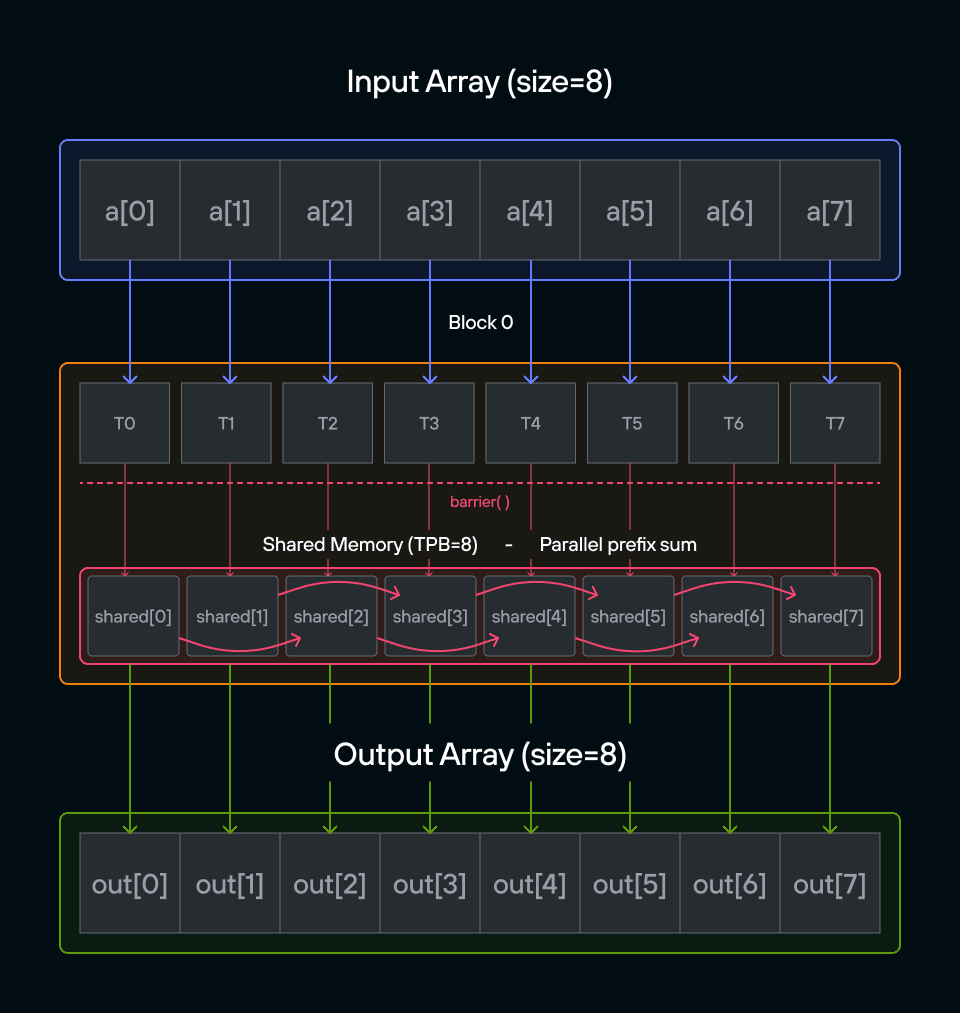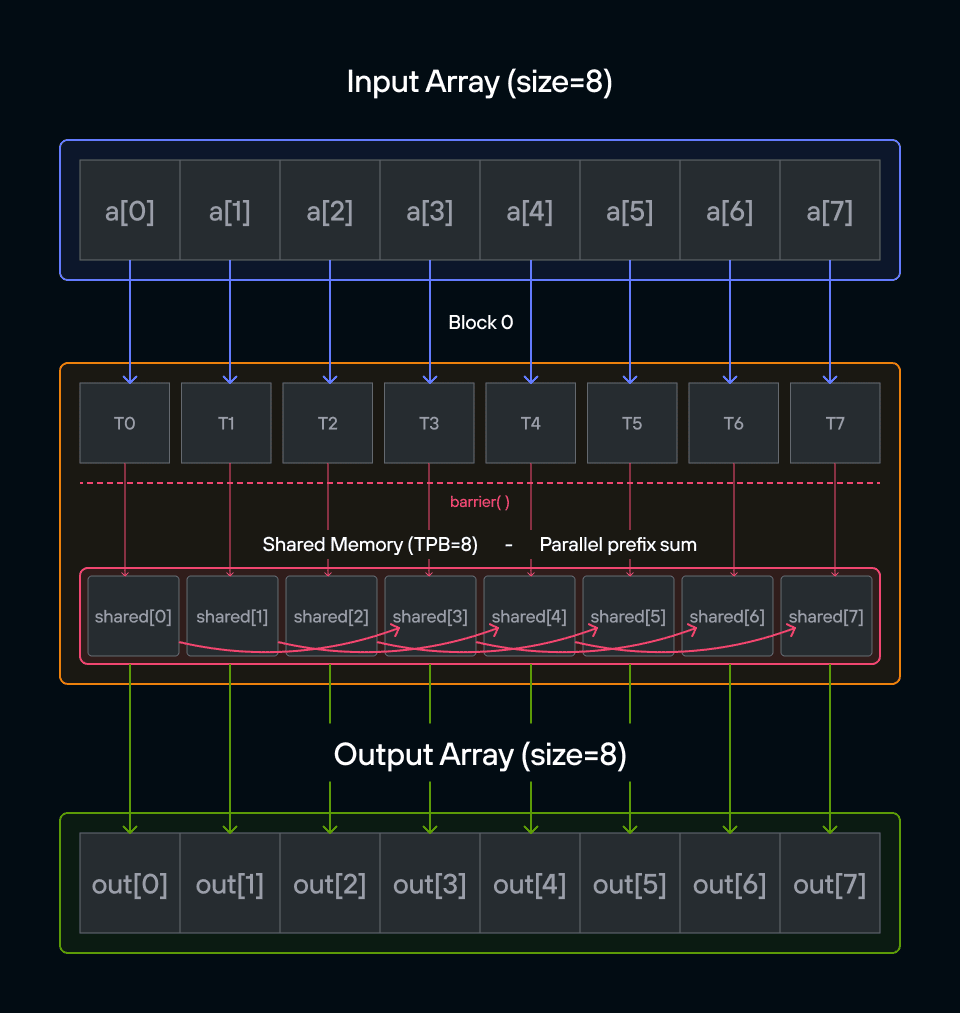
Key concepts

In this puzzle, you’ll learn about:

• Parallel algorithms with logarithmic complexity
• Shared memory coordination patterns
• Multi-phase computation strategies

The key insight is understanding how to transform a sequential operation into an efficient parallel algorithm using shared memory.

For example, given an input sequence \([3, 1, 4, 1, 5, 9]\), the prefix sum would produce:

• \([3]\) (just the first element)
• \([3, 4]\) (3 + 1)
• \([3, 4, 8]\) (previous sum + 4)
• \([3, 4, 8, 9]\) (previous sum + 1)
• \([3, 4, 8, 9, 14]\) (previous sum + 5)
• \([3, 4, 8, 9, 14, 23]\) (previous sum + 9)

Mathematically, for a sequence \([x_0, x_1, …, x_n]\), the prefix sum produces: \[[x_0, x_0+x_1, x_0+x_1+x_2, …, \sum_{i=0}^n x_i] \]

While a sequential algorithm would need \(O(n)\) steps, our parallel approach will use a clever two-phase algorithm that completes in \(O(\log n)\) steps! Here’s a visualization of this process:

Step 1 of 3

Step 2 of 3

Step 3 of 3

This puzzle is split into two parts to help you learn the concept:

• Simple Version Start with a single block implementation where all data fits in shared memory. This helps understand the core parallel algorithm.

• Complete Version Then tackle the more challenging case of handling larger arrays that span multiple blocks, requiring coordination between blocks.

Each version builds on the previous one, helping you develop a deep understanding of parallel prefix sum computation. The simple version establishes the fundamental algorithm, while the complete version shows how to scale it to larger datasets - a common requirement in real-world GPU applications.